Merge And Quick Sort

Merge Sort

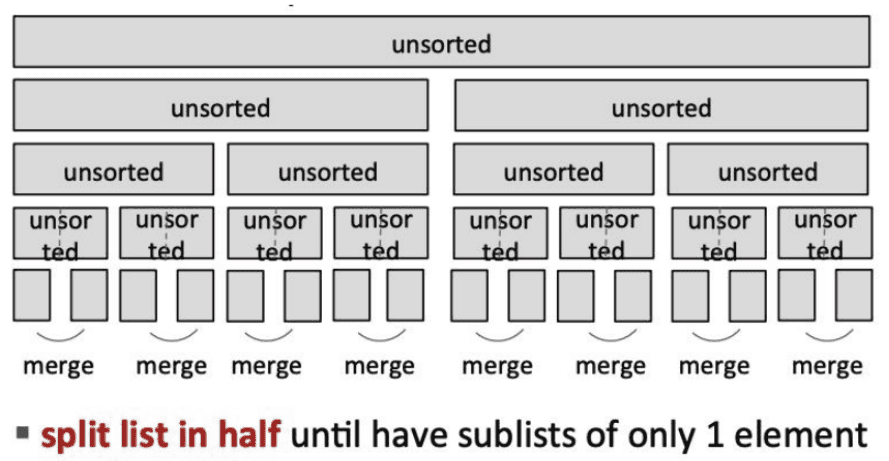
• If the list is of len 0 or 1 => already sorted, do nothing
• If the list has > 1 element, split into 2 lists and sort each
• Merge 2 sorted sublists (use the above solution)

Time: O(n log n)

• O(logn) recursion level
• O(n) for each recursion level => this part is for merging 2 sorted array

Space: O(n)

function mergeSort(arr) {
    if (arr.length <= 1) {
        return arr;
    }

    const middle = Math.floor(arr.length / 2);
    const left = arr.slice(0, middle);
    const right = arr.slice(middle);

    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
    let result = [];
    let leftIndex = 0;
    let rightIndex = 0;

    while (leftIndex < left.length && rightIndex < right.length) {
        if (left[leftIndex] < right[rightIndex]) {
            result.push(left[leftIndex]);
            leftIndex++;
        } else {
            result.push(right[rightIndex]);
            rightIndex++;
        }
    }

    return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}

// Example usage:
const array = [5, 3, 8, 4, 2, 7, 1];
const sortedArray = mergeSort(array);
console.log(sortedArray); // Output: [1, 2, 3, 4, 5, 7, 8]

Quick Sort

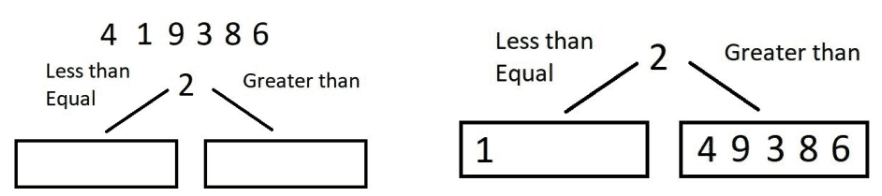
• Create 2 arrays to hold elements less than the pivot value and elements greater than the pivot value.

• Recursively sort the sub arrays.

• Time Complexity:

  • Worst case: O(n) + O(n-1) + O(n-2) + … + O(1) = O((n+1)*n/2) = O(n^2). When array is already sorted
  • Best case: O(nlogn). When the pivot is always the median of the array
  • Average case: O(nlogn). Choose pivot as a random number in the array

• Space

  • Each recursion step: O(1) space (Dutch flag partition use O(1) extra space)
  • logn time of recursion => O(logn) space in total

function quickSort(arr) {
    if (arr.length <= 1) {
        return arr;
    }

    const pivot = arr[Math.floor(arr.length / 2)];
    const left = [];
    const right = [];

    for (let i = 0; i < arr.length; i++) {
        if (i === Math.floor(arr.length / 2)) {
            continue;
        }
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }

    return [...quickSort(left), pivot, ...quickSort(right)];
}

// Example usage:
const array = [5, 3, 8, 4, 2, 7, 1];
const sortedArray = quickSort(array);
console.log(sortedArray); // Output: [1, 2, 3, 4, 5, 7, 8]

Quick Sort vs Merge Sort

• Merge Sort is a stable algorithm (O(nlogn) all the time)
• Quick Sort is unstable algorithm (O(nlogn) => O(n^2) worst case)
• Quick Sort only works well on random access collection (array). So when sorting linked list or doubly linked list => use Merge Sort
• when sorting a linked list using Quick Sort: choosing a random pivot is very slow as we do not have random access

Quick Select

• Find the K-th smallest element in an unsorted list

• We can use the Quick Sort idea:

  • First set K = K - 1. Kth smallest number will be at (K-1) index in the sorted array.
  • Choose a pivot (randomly) and apply the Dutch partition => after this, we know the pivot index.
    • if the index of the pivot == K, we found the K-th smallest element, just return it
    • if the index of the pivot < K, recurs for the left part
    • if the index of the pivot > K, recurs for the right part

• Average case: O(n)

• Worst case: O(n) + O(n-1) + O(n-2) + … + O(1) = O(n^2)

• Best case: O(n) + O(n/2) + O(n/4) + … + O(1) = O(n * (1+½+¼+⅛+…)) = O(n)

Question: Why the QuickSelect best case is better than QuickSort best case?

Because in QuickSelect, we only need to process the left or right sublist after each recursion. In QuickSort, we have to process both the left and right sublists.

Counting Sort

• Idea: count the frequency of each element in the list, then build the result

A = [ 1, 9, 1, 3, 9, 4, 10, 100]
Count: hashmap from value => frequency
Count[4] = 1
Count[1] = 2 ;
Count[3] = 1 ;
Count[10] = 1 ;
Count[100] = 1 ;
Count[9] = 2

• Runtime: O(n+ maxValue - minValue + 1)

• Space: O(n)

• when to use: range is small enough. e.g 0 <= a[i] <= 10000 => O(n+10000) << O(nlogn).

• when cannot use:

  • a[i] is too big ( -10^9 <= a[i] <= 10^9)
  • a[i] is not integer (double, object)